실수의 부정확함
- 컴퓨터는 모든 데이터를 0과 1로밖에 표현할 수 없다 (bit)
- 인간이 이해할 수 있는 소수점을 포함한 실수는..?
사실 프로그램에선 그 유사값으로 보여주는 경우가 매우 많다. - 정확한 문서는 아래 링크를 참고하자 IEEE754
- 진짜 학회 문서는 돈주고 사야되는건가봄.. 😅
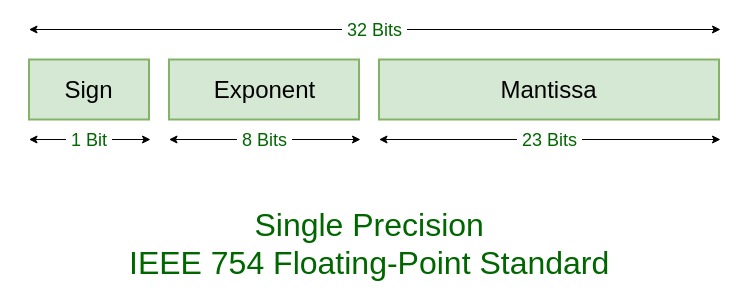
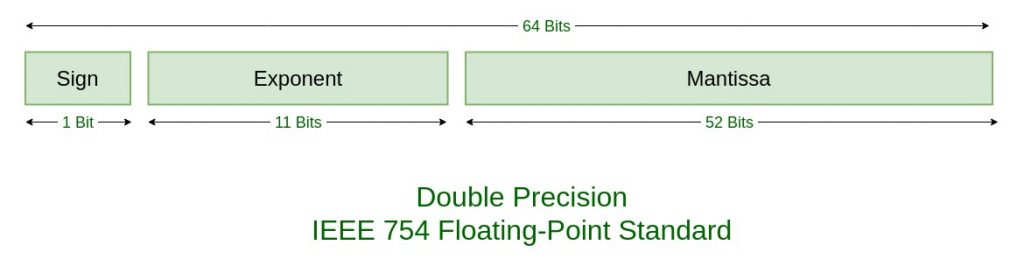
- Sign 은 부호 표시
- Exponent는 지수 부분
- Mantissa는 가수 부분
- 결국 수학적으로 가수부분은 2^-1, 2^-2….로 밖에 표현을 못하기때문에,
근사값을 나타낼순 있지만 정확한 수는 표현 못함- 16bit -> 32bit -> 64bit로 갈수록 정확한 값에 근사 하겠으나 동일한 값은 절대 될 수 없다.
-
특히 0.1 같은 순환 소수라면 100% 오차가 발생
- 짧게 보기 좋은 유튜브 영상 참고!
출처 자료
Divide By Zero 문제
정수를 0으로 나눌 때의 문제
- (수학적으로) 정수 0으로 나누기는 결과에 대한 정수 표현이 아예 없다.
- 정수를 없는것으로 나눈다면 그것을 어떤 정수 표현해야 할까..? 표현이 없음.
- 일반적 계산기에서 0으로 나눈다면, 작동이 중지되고 오류메시지가 표시된다.
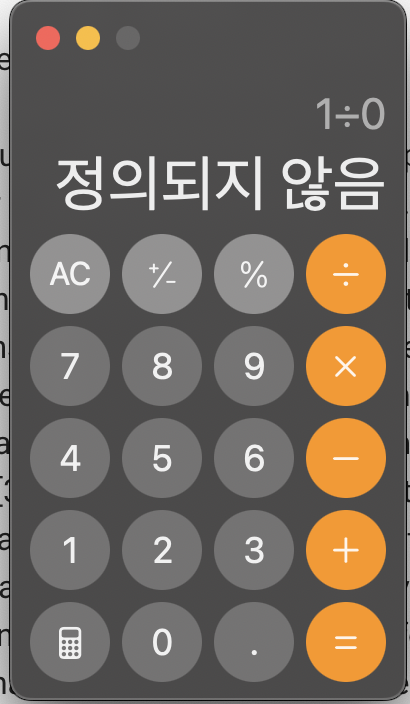
고전적 프로그래밍에서 0으로 나눌때 구현?
- 8 / 2를 구현한다면? 8-2-2-2-2가 0이 나올때 까지 계산한다.
- 그런데 8 / 0 일때는..? 8-0-0-0-0…. 무한루프가 발생한다.
- 프로그램 과열, 원치않은 연산이 반복된다
- 프로그래밍 언어에서 Exception 처럼 0으로 나눌때 미리 분모가 0임을 확인해서 계산이 아예 일어나지 않도록 바꾼다.
- 혹은 현대 OS에서 인터럽트가 발생하여 OS에서 적절하게 처리해서 프로세스에 전달한다.
부동 소수점 나눌 때의 문제
- 정수형이 아니라 부동 소숫점에서의 나눗셈 연산에서는?
- 0으로 출력할경우 에러를 출력하는 대신, 무한대 (∞, -∞) 혹은 Nan(Not a number)를 출력한다.
- C++ 에서는 부동소숫점을 0으로 나눌경우 무한대로,
왜냐면 부동소수점으로 표현한 0을 0이아니라 0에 근접한 어떠한 수로 취급하기 때문 - 프로그래밍에서 다룰 수 없는 아주 작은수는 0, 다룰 수 없을 정도로 아주 큰 수는 무한대로 표현한다.
- C++ 에서는 부동소숫점을 0으로 나눌경우 무한대로,
옛날 기계식 계산기에서 0으로 나눴을때 - 무한 루프 발생
- 프로그램의 안정적인 구동을 위해서라도, 프로그래밍에서도 0으로 나눌때 예외적인 처리가 필요함.