Tree
- 부모노드와 자식노드로 구성.
- 부모에서 자식으로 계층적으로 이어진 데이터 구조를 트리라고 한다.
트리도 방향이 있는데 왜 선형적이라고 하지 않는것인가?
- 데이터가 순차적인 방식으로 저장되지 않는다. (선형적으로 저장되는것이 아님)
- 선형적인 데이터 구조들은 .next 와 같은 일관적인 방법으로 다음에 접근 할 수있는데, 비선형적인 애들은 뭔가 조건을 봐야됨 (순회시에 조건이 필요함)
- 선형과 비선형의 차이
Tree 자료구조의 유형
- Non-binary Tree
- 자식이 2개 이상인 트리
- B-tree, 2-3-4 tree
- 보는것부터 어지럽다..
- 근데 아직까지 쓰는곳을 별로 못보긴함.. 다행인가..?
- 자식이 2개 이상인 트리
- Binary Tree
- 부모 - 자식 노드가 2개로 구성되어있을때 이진 트리.
- 없는 (null) 노드도 노드로 볼수 있기 때문에, 한쪽으로만 쭉 있어도 이진트리다.
- 포화 이진 트리 - 모든 레벨의 노드가 빈틈없이 꽉 차있을때 (추가하려면 높이를 높여야할때)
- 완전 이진 트리 - 모든 레벨은 아니지만 자식 노드가 아무튼 꽉차있을때
- 왜 굳이 이진 트리를 써야하는가?
- 이진 트리 형태로 되어있으면 자료 탐색할때 매우 좋다.
- (트리가 균형잡혔다고 가정했을때) 자료를 탐색할때의 시간이 log N으로 보장된다.
- 자료의 삽입 기준은 단순.
- 현재 노드와 찾는 값을 비교해서 작으면 왼쪽노드 크면 오른쪽 노드로 가면 됨.
- Binary Search Tree, AVL Tree, Red Black Tree 등등 많은 종류의 알고리즘들이 있다.
- 부모 - 자식 노드가 2개로 구성되어있을때 이진 트리.
트리의 균형이 깨지는 케이스
- 이진탐색트리

- 이렇게 이진 트리가 좋아 보이지만 최악의 경우 위처럼 리스트나 배열을 쓰는것과 다름없는 트리가 나올수도 있다.
- 특히 정렬이 된 자료를 이진 검색 트리로 다시 넣는다면? 무조건 안좋게 나올것임 (배열을 탐색하는것과 다름이 없다)
C# 에서 구현된 트리 형태의 자료구조?
- SortedSet -> Red Black Tree로 구현됨
- 자동으로 트리의 높이를 균형 잡아주는 레드 블랙 트리 알고리즘을 C#에서도 쓰고있다!
- 트리 리프 노드간 최대 깊이의 차이가 2 이상 차이 나지 않도록 하는것. 자세한것은 따로 찾아보는게 좋을듯.
- RedBlackTree
// SortedSet 의 일부. 이것만 봐도 아마 레드블랙 트리인것 같다.
internal virtual bool AddIfNotPresent(T item)
{
if (this.root == null)
{ this.root = new SortedSet<T>.Node(item, NodeColor.Black);
this.count = 1;
++this.version;
return true;
} SortedSet<T>.Node current1 = this.root;
SortedSet<T>.Node parent = (SortedSet<T>.Node) null;
SortedSet<T>.Node grandParent = (SortedSet<T>.Node) null;
SortedSet<T>.Node greatGrandParent = (SortedSet<T>.Node) null;
++this.version;
int num = 0;
for (; current1 != null; current1 = num < 0 ? current1.Left : current1.Right)
{ num = this.comparer.Compare(item, current1.Item);
if (num == 0)
{ this.root.ColorBlack();
return false;
} if (current1.Is4Node)
{ current1.Split4Node();
if (SortedSet<T>.Node.IsNonNullRed(parent))
this.InsertionBalance(current1, ref parent, grandParent, greatGrandParent);
} greatGrandParent = grandParent; grandParent = parent; parent = current1; } SortedSet<T>.Node current2 = new SortedSet<T>.Node(item, NodeColor.Red);
if (num > 0)
parent.Right = current2;
else
parent.Left = current2;
if (parent.IsRed)
this.InsertionBalance(current2, ref parent, grandParent, greatGrandParent);
this.root.ColorBlack();
++this.count;
return true;
}
트리의 삽입시 일어나는 회전이 너무 어렵다.. ㅠㅠ
- AVL트리, REDBLACK트리
- LL회전, LR회전, RL회전, RR회전 등을 통해 트리의 균형을 맞출수 있다.
- 어떻게 어떻게 AVL 트리는 까지는 이해함 (구현 X)
- 위 회전들을 케이스에 맞게 사용한다면, 결국 균형잡힌 트리를 만들 수 있다 (AVL 트리의 알고리즘)
- 그러나 삽입 삭제가 모든 트리에서 일어날 수 있는것이 단점. (대신 더 균형이 잡혀있는 트리이다.)
- 레드블랙 트리는 뭔가 조건이 더 있고, 삽입 삭제시 트리가 회전하는것을 줄이기 위해 색깔 플래그와 조건들이 있는걸로 보이는데.. 더 이해 한다면 추가로 정리해보겠슴…
Graph
C#에서 직접 구현된 자료구조는 없음.
- 구현하려면 직접 만들어야된다.
- Node(vertex)와 Edge로 이뤄진 자료구조, 방향이나 가중치가 추가될 수 있음.
- 소셜 네트워크나 네비게이션 길찾기 등에서 사용
그래프 탐색 (순회) 알고리즘
- 한번 방문한 노드를 저장해서 다시 방문하지 않도록 해야함
- 그렇지 않으면 순환 그래프 (지하철 2호선 같은..) 일 경우 무한루프에 빠질수 있다.
BFS - 너비 우선 탐색
- Queue를 이용해서 보통 해결한다.
- 루트 노드에서 아래로 내려간후, 형제 노드들 부터 먼저 탐색, 모두 탐색했으면 다시 아래로 내려감
- 가장 짧은 길 탐색 할때 적용
- 범위 내 가장 가까이 있는 적
- 거리에 기준 도달 가능하는 영역 판별 등
- 단점 : 탐색해야할 모든 대상들을 큐에 넣어야 하기 때문에, 메모리 문제가 될 수 있음
DFS - 깊이 우선 탐색
- 스택 혹은 재귀함수로 구현
- 자식 노드의 한쪽 방향으로 쭉 내려가서 리프이면 다시 위로 올라가는 탐색을 반복한다.
- 모든 경우의 수 탐색
- 유효성 검사 (가능한지 불가능한지)
- 시뮬레이션 게임에서 경우의 수들 탐색할때
- 그래프가 너무 클때도 사용. (BFS로 다 탐색하기가 힘들때?)
- 단점! 목표 노드가 없는 뎁스가 긴 하위 트리로 들어가게 되었을때, 불필요한 탐색을 많이 수행할 수 있음.
번외 : 모든 경우의 수를 탐색할때 DFS를 쓴다..?
- 모든 경우의 수를 탐색한다 -> BFS도 보면 결국 모든 경우의 수를 탐색하는데 쓸 수 있는데 무슨 차이인가?
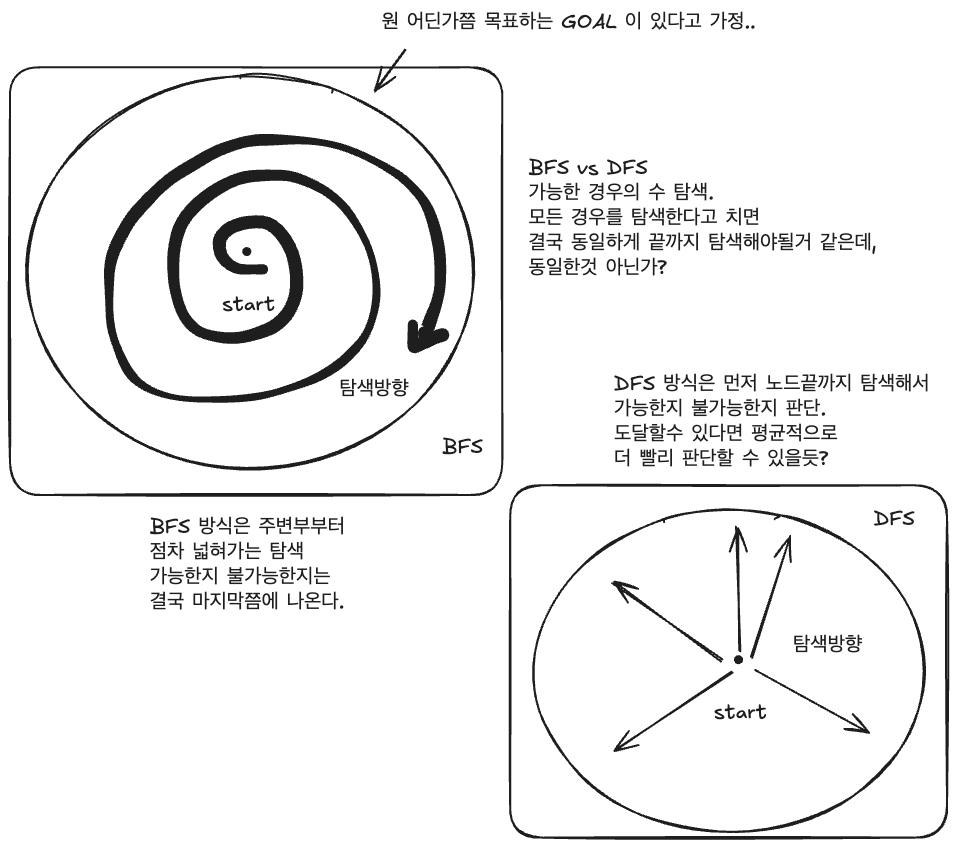
그래프가 너무 클때? (깊이나 너비가 너무 넓다!)
- 깊이를 제한해서 탐색하는 방법이 적당함.
- 어느정도 깊이를 탐색한후 더이상 찾는 노드가 없으면 옆의 노드로 넘어가는?
Depth Limited Search - 깊이 제한 탐색?
- DFS와 작동 방식은 똑같지만, 깊이를 끝까지 들어가지 않고 한계 깊이를 정해 그 이상 탐색하지 않고 넘어간다.
IDS (Iterrative Deepening Search) 작동방식
- 위의 Depth Limited Search와 비슷하게 동작
- 그러나 뎁스를 한단계씩 늘려나가면서 탐색하는 것으로 변경
- ex) 뎁스 5 -> 10 -> 15 등으로 늘릴수 있을듯?
- 잘 된다면 DFS의 메모리를 작게 쓴다는 장점과 BFS의 장점을 합친 결과가 나올.. 지도?